Thoughts on paper Provable Limitations of Acquiring Meaning from Ungrounded Form: What will Future Language Models Understand? and beyond.

The Question

Can language meaning be learned from form alone?

This is arguably the philosophial question most relevant to today’s NLP, asking if its data-driven paradigm is fundamentally sound. It sure feels politically correct to say no, but the detailed arguments and counter-arguments have produced a great debate.

My personal take:

• Representations from learning on corpus (word2vec, BERT contextual embeddings) are obviously meaningful. I still remember the shock many years ago seeing king - man + woman = queen.
• But whether such models have learned meaning require probing tasks that specify how a model shall behave if it learns language meaning. On many tasks (dialogue, storytelling, …) current NLP models perform poorly, and even huger corpus doesn’t seem a path to solving these.
• The tricky thing about probing tasks is that, your model will always get grounded when fine-tuned - you gain inductive bias about task intent through new data or new optimization or new parameters. In a sense, a toehold of grounding (or inductive bias) bootstraps the learning of meaning (and pre-training might make learning much faster and easier). But no matter how much power you gain from pre-training on form alone, you just can’t jump without a toehold of ground to jump from!
  • The empirical question is how large the toehold should be, so that empirical numbers make most sense.
  • The theoretical question is: how small the toehold could be, so that learning meaning can be bootstrapped?

Provable Limitations of Acquiring Meaning from Ungrounded Form: What will Future Language Models Understand? is an interesting step toward the theoretical question. It argues meaning cannot be learned even with a seemingly huge toehold: the ability to query oracle if two texts have the same (contextual) meaning.

The Setup

You can’t learn a Python compiler from just seeing Python code, since you don’t get to obserse any input/output execution results. But what if code is equipped with assertions?

a = 3 + 5
assert a == 8

You may learn some meaning from it!

To be even more generuous, assume assertions are on your side. You get to choose two strings x and y to query, and assertion assert x == y tell you if they evaluate to the same value within their respective context.

For example, let x be

a += 5

and let y be

a += 2; if True: a += 3

They should be equivalent no matter what code precedes them, therefore they should have the same representation.

The task is, assign each string x a representation f(x) , so that for any two strings, f(x)=f(y) iff assert x==y holds for all (valid) contexts.

A projection back to the meaning-probing-grounding framework:

• Added probe data? Unlimited, as long as you can process in computable time. Or equivalently, your original corpus is designed best for you and you have zero new data.
• Added probe power? Unlimited, in the sense that probe family is any function and you can choose the best function out of any function. Or equivalently, there is not probe learning, just about existance.
• Added anything else? **Understand the meaning of word assert and the meaning of it combined with arbitrary statements **. That’s the only toehold from form to meaning in the setup.
• Also note task is kind of harsh, you need representations to respect contextual equivalence for all strings and all contexts.

The Proof

The idea of the proof is quite simple. Consider Python programs looking like either left or right, where m and n can be seen as integer constants. Here tm_run is essentially an Universal Turing Machine that takes Turing machine state m and returns Turing machine state n steps later.

• Oracle has no computability beyond Turing Machine, because for each concrete n, both programs can be run in finite time and compared.
• “Emulating meaning” requires solving the halting problem (for every m) and is not computable, because for a fixed m, if

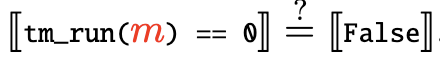
holds, it means it holds for all n, i.e. Turing Machine m does not halt. You simply can’t do that if your oracle isn’t beyond Turing Machine.

Back to The Setup

I feel the main proof is rather tricky than insightful, and here are a few comments:

• Humans also cannot “emulate meaning” in such a setup, since we can’t solve the halting problem either?

• The considered language is too weak - just a tiny subset of possible Python programs, so that it makes oracle weaker (within TM) and task easier (but still beyond TM).

• Power about language is you can talk about language itself, and that’s the essence of Turing Machine. In a “complete” language, from assertion

  Program m cannot halt in any finite steps
  

  you can gain meaning about program m. This is because you understand meanings of extra things like “any” or “finite”. So perhaps minimal grounding requires knowing meaning beyond assert - maybe some other elements like or any if……

Back to The Question

• Theoretical question is hard, not yet well-defined. This paper seems to brings more question than answers.
  • Better setup or definition for “learning meaning” and “grounding” might be needed.
  • Especially, in language of logic, grounding and inductive bias are very similar, and are very tricky.
• Theoretical question might not be related to the empirical question (yet), especially when the theoretical question leads to negative answers.
  • Theory may not have been well-established, and setups are far from practice.
  • Even if the theory is well-established, think of worse-case time complexity analysis vs. practicatily of some algorithm.
• Key aspects about learning from form are still missing: modelling token co-occurance, for example, is not even touched in the paper. How co-occurance statistics lead to “structure” is still intriguing.